Filters
Question type
Study Flashcards

Describe the transformations and give the equation for the graph. - Describe the transformations and give the equation for the graph. - A) It is the graph of \mathrm { f } ( \mathrm { x } ) = \sqrt { \mathrm { x } } translated 4 units to the right, stretched vertically by a factor of 3 and translated 2 units up. The equation is y = 3 \sqrt { x - 4 } + 2 B) It is the graph of f ( x ) = \sqrt { x } translated 4 units to the right, shrunken vertically by a factor of \frac { 1 } { 3 } and translated 2 units up. The equation is y = \frac { 1 } { 3 } \sqrt { x + 4 } + 2 C) It is the graph of f ( x ) = \sqrt { x } translated 4 units to the right, shrunken vertically by a factor of \frac { 1 } { 3 } and translated 2 units up. The equation is y = \frac { 1 } { 3 } \sqrt { x - 4 } + 2 D) It is the graph of f ( x ) = \sqrt { x } translated 4 units to the right, stretched vertically by a factor of 3 and translated 2 units up. The equation is y = 3 \sqrt { x + 4 } + 2


A) It is the graph of f(x) =x\mathrm { f } ( \mathrm { x } ) = \sqrt { \mathrm { x } } translated 4 units to the right, stretched vertically by a factor of 3 and translated 2 units up. The equation is y=3x−4+2y = 3 \sqrt { x - 4 } + 2
B) It is the graph of f(x) =xf ( x ) = \sqrt { x } translated 4 units to the right, shrunken vertically by a factor of 13\frac { 1 } { 3 } and translated 2 units up. The equation is y=13x+4+2y = \frac { 1 } { 3 } \sqrt { x + 4 } + 2
C) It is the graph of f(x) =xf ( x ) = \sqrt { x } translated 4 units to the right, shrunken vertically by a factor of 13\frac { 1 } { 3 } and translated 2 units up. The equation is y=13x−4+2y = \frac { 1 } { 3 } \sqrt { x - 4 } + 2
D) It is the graph of f(x) =xf ( x ) = \sqrt { x } translated 4 units to the right, stretched vertically by a factor of 3 and translated 2 units up. The equation is y=3x+4+2y = 3 \sqrt { x + 4 } + 2

E) A) and B)
F) C) and D)

Correct Answer

verifed

verified

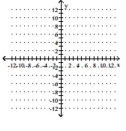
Graph the point symmetric to the given point. -  Plot the point (0,−7) , then plot the point that is symmetric to (0,−7)  with respect to the y-axis. \text { Plot the point } ( 0 , - 7 ) \text {, then plot the point that is symmetric to } ( 0 , - 7 ) \text { with respect to the } y \text {-axis. } Graph the point symmetric to the given point. - \text { Plot the point } ( 0 , - 7 ) \text {, then plot the point that is symmetric to } ( 0 , - 7 ) \text { with respect to the } y \text {-axis. } A) B) C) D)


A)
Graph the point symmetric to the given point. - \text { Plot the point } ( 0 , - 7 ) \text {, then plot the point that is symmetric to } ( 0 , - 7 ) \text { with respect to the } y \text {-axis. } A) B) C) D)

B)
Graph the point symmetric to the given point. - \text { Plot the point } ( 0 , - 7 ) \text {, then plot the point that is symmetric to } ( 0 , - 7 ) \text { with respect to the } y \text {-axis. } A) B) C) D)

C)
Graph the point symmetric to the given point. - \text { Plot the point } ( 0 , - 7 ) \text {, then plot the point that is symmetric to } ( 0 , - 7 ) \text { with respect to the } y \text {-axis. } A) B) C) D)

D)
Graph the point symmetric to the given point. - \text { Plot the point } ( 0 , - 7 ) \text {, then plot the point that is symmetric to } ( 0 , - 7 ) \text { with respect to the } y \text {-axis. } A) B) C) D)



E) A) and B)
F) B) and C)

Correct Answer

verifed

verified

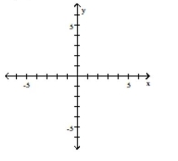
Graph the function. - f(x) =∣4x∣f(x) =|4 x| Graph the function. - f(x) =|4 x| A) B) C) D)


A)
Graph the function. - f(x) =|4 x| A) B) C) D)

B)
Graph the function. - f(x) =|4 x| A) B) C) D)
C)
Graph the function. - f(x) =|4 x| A) B) C) D)

D)
Graph the function. - f(x) =|4 x| A) B) C) D)

E) C) and D)
F) B) and D)

Correct Answer

verifed

verified

Give the domain and range of the relation. - x=y2x = y ^ { 2 }


A) domain: (∞,∞) ( \infty , \infty ) ; range: (−∞,∞) ( - \infty , \infty )
B) domain: [0,∞) [ 0 , \infty ) ; range: [0,∞) [ 0 , \infty )
C) domain: (∞,∞) ( \infty , \infty ) ; range: [0,∞) [ 0 , \infty )
D) domain: [0,∞) [ 0 , \infty ) ; range: (−∞,∞) ( - \infty , \infty )

E) A) and B)
F) None of the above

Correct Answer

verifed

verified

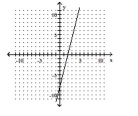
The graph of a linear function f is shown. Identify the slope, y-intercept, and x-intercept. - The graph of a linear function f is shown. Identify the slope, y-intercept, and x-intercept. - A) \frac { 1 } { 4 } ; ( 0 , - 8 ) , ( 2,0 ) B) 4 ; ( 0 , - 8 ) , ( 2,0 ) C) \frac { 1 } { 4 } ; ( 0,2 ) , ( - 8,0 ) D) 4 ; ( 0,2 ) , ( - 8,0 )


A) 14;(0,−8) ,(2,0) \frac { 1 } { 4 } ; ( 0 , - 8 ) , ( 2,0 )
B) 4;(0,−8) ,(2,0) 4 ; ( 0 , - 8 ) , ( 2,0 )
C) 14;(0,2) ,(−8,0) \frac { 1 } { 4 } ; ( 0,2 ) , ( - 8,0 )
D) 4;(0,2) ,(−8,0) 4 ; ( 0,2 ) , ( - 8,0 )

E) None of the above
F) A) and D)

Correct Answer

verifed

verified

Describe how the graph of the equation relates to the graph of y y=x3y = \sqrt [ 3 ] { x } - Describe how the graph of the equation relates to the graph of y y = \sqrt [ 3 ] { x } - A) y = ( x - 3 ) ^ { 2 } B) y = x ^ { 2 } - 3 C) y = x ^ { 2 } + 3 D) y = ( x + 3 ) ^ { 2 }


A) y=(x−3) 2y = ( x - 3 ) ^ { 2 }
B) y=x2−3y = x ^ { 2 } - 3
C) y=x2+3y = x ^ { 2 } + 3
D) y=(x+3) 2y = ( x + 3 ) ^ { 2 }

E) B) and C)
F) None of the above

Correct Answer

verifed

verified

Provide an appropriate response. -If the point (a, b) is in the fourth quadrant, in what quadrant is (a, -b) ?


A) I
B) III
C) IV
D) II

E) B) and C)
F) A) and D)

Correct Answer

verifed

verified

Find the slope of the line satisfying the given conditions. -through (3, -8) and (3, 6)


A) 14
B) undefined
C) -14
D) 0

E) B) and D)
F) A) and C)

Correct Answer

verifed

verified

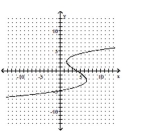
Decide whether the relation defines a function. -Decide whether the relation defines a function. - A) Function B) Not a function


A) Function
B) Not a function

C) A) and B)
D) undefined

Correct Answer

verifed

verified

Graph the function. - f(x) =⟦x]−1f(x) =\llbracket x]-1 Graph the function. - f(x) =\llbracket x]-1 A) B) C) D)


A)
Graph the function. - f(x) =\llbracket x]-1 A) B) C) D)

B)
Graph the function. - f(x) =\llbracket x]-1 A) B) C) D)

C)
Graph the function. - f(x) =\llbracket x]-1 A) B) C) D)

D)
Graph the function. - f(x) =\llbracket x]-1 A) B) C) D)

E) A) and C)
F) B) and C)

Correct Answer

verifed

verified

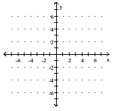
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such. - g(x) =x+2g ( x ) = x + 2 Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such. - g ( x ) = x + 2 A) D = ( - \infty , \infty ) , R = ( - \infty , \infty ) B) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) C) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) D) D = ( - \infty , \infty ) , R = ( - \infty , \infty )


A) D=(−∞,∞) ,R=(−∞,∞) D = ( - \infty , \infty ) , R = ( - \infty , \infty )
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such. - g ( x ) = x + 2 A) D = ( - \infty , \infty ) , R = ( - \infty , \infty ) B) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) C) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) D) D = ( - \infty , \infty ) , R = ( - \infty , \infty )

B) D=(−∞,∞) ,R=(−∞,∞) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty )
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such. - g ( x ) = x + 2 A) D = ( - \infty , \infty ) , R = ( - \infty , \infty ) B) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) C) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) D) D = ( - \infty , \infty ) , R = ( - \infty , \infty )
C) D=(−∞,∞) ,R=(−∞,∞) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty )
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such. - g ( x ) = x + 2 A) D = ( - \infty , \infty ) , R = ( - \infty , \infty ) B) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) C) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) D) D = ( - \infty , \infty ) , R = ( - \infty , \infty )

D) D=(−∞,∞) ,R=(−∞,∞) D = ( - \infty , \infty ) , R = ( - \infty , \infty )
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such. - g ( x ) = x + 2 A) D = ( - \infty , \infty ) , R = ( - \infty , \infty ) B) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) C) \mathrm { D } = ( - \infty , \infty ) , \mathrm { R } = ( - \infty , \infty ) D) D = ( - \infty , \infty ) , R = ( - \infty , \infty )

E) B) and C)
F) A) and D)

Correct Answer

verifed

verified

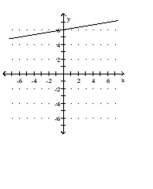
The graph of a linear function f is shown. Write the equation that defines f. Write the equation in slope-intercept form. - The graph of a linear function f is shown. Write the equation that defines f. Write the equation in slope-intercept form. - A) y = \frac { 1 } { 6 } x + 6 B) y = \frac { 1 } { 6 } x - 6 C) y = 6 x - 6 D) y = 6 x + 6


A) y=16x+6y = \frac { 1 } { 6 } x + 6
B) y=16x−6y = \frac { 1 } { 6 } x - 6
C) y=6x−6y = 6 x - 6
D) y=6x+6y = 6 x + 6

E) A) and C)
F) A) and B)

Correct Answer

verifed

verified

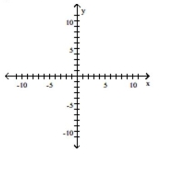
Graph the function. - y=(x+3) 3y=(x+3) ^{3} Graph the function. - y=(x+3) ^{3} A) B) C) D)


A)
Graph the function. - y=(x+3) ^{3} A) B) C) D)

B)
Graph the function. - y=(x+3) ^{3} A) B) C) D)
C)
Graph the function. - y=(x+3) ^{3} A) B) C) D)

D)
Graph the function. - y=(x+3) ^{3} A) B) C) D)

E) A) and B)
F) B) and C)

Correct Answer

verifed

verified

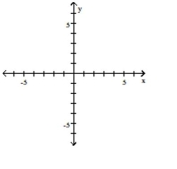
Graph the function. - f(x) =12x3f ( x ) = \frac { 1 } { 2 } x ^ { 3 } Graph the function. - f ( x ) = \frac { 1 } { 2 } x ^ { 3 } A) B) C) D)


A)
Graph the function. - f ( x ) = \frac { 1 } { 2 } x ^ { 3 } A) B) C) D)

B)
Graph the function. - f ( x ) = \frac { 1 } { 2 } x ^ { 3 } A) B) C) D)
C)
Graph the function. - f ( x ) = \frac { 1 } { 2 } x ^ { 3 } A) B) C) D)

D)
Graph the function. - f ( x ) = \frac { 1 } { 2 } x ^ { 3 } A) B) C) D)

E) B) and C)
F) A) and D)

Correct Answer

verifed

verified

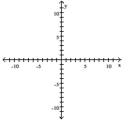
Find the slope of the line and sketch the graph. - y=5xy=5 x Find the slope of the line and sketch the graph. - y=5 x A) m = 5 B) m = \frac { 1 } { 5 } C) m = - 5 D) m = 0


A) m=5m = 5
Find the slope of the line and sketch the graph. - y=5 x A) m = 5 B) m = \frac { 1 } { 5 } C) m = - 5 D) m = 0

B) m=15m = \frac { 1 } { 5 }
11ed7969_2718_1517_9733_714f2487f5af_TB7514_11
C) m=−5m = - 5
11ed7969_3107_6ad9_9733_95c2c9021dc0_TB7514_11

D) m=0m = 0
11ed7969_3632_f6fa_9733_7b5103f60b8e_TB7514_11

E) All of the above
F) B) and D)

Correct Answer

verifed

verified

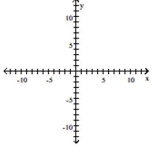
Graph the function. - y=3x2−1y=3 x^{2}-1 Graph the function. - y=3 x^{2}-1 A) B) C) D)


A)
Graph the function. - y=3 x^{2}-1 A) B) C) D)

B)
Graph the function. - y=3 x^{2}-1 A) B) C) D)
C)
Graph the function. - y=3 x^{2}-1 A) B) C) D)

D)
Graph the function. - y=3 x^{2}-1 A) B) C) D)

E) A) and D)
F) A) and B)

Correct Answer

verifed

verified

Determine whether the equation has a graph that is symmetric with respect to the y-axis, the x-axis, the origin, or none of these. - y=0.11x4+x2+6y = 0.11 x ^ { 4 } + x ^ { 2 } + 6


A) origin only
B) none of these
C) yy -axis only
D) x-axis only

E) C) and D)
F) A) and B)

Correct Answer

verifed

verified

Find the slope and the y-intercept of the line. - y−4x+3=0y - 4 x + 3 = 0


A) slope: 3;y3 ; y -intercept: (0,−4) ( 0 , - 4 )
B) slope: 4 ; y-intercept: (0,3) ( 0,3 )
C) slope: −3;y- 3 ; y -intercept: (0,4) ( 0,4 )
D) slope: 4;y4 ; y -intercept (0,−3) ( 0 , - 3 )

E) A) and B)
F) All of the above

Correct Answer

verifed

verified

Give the domain and range of the relation. - Give the domain and range of the relation. - A) domain: ( - \infty , - 2 ) \cup ( - 2 , \infty ) ; range: ( - \infty , 0 ) \cup ( 0 , \infty ) B) domain: ( - \infty , \infty ) ; range: ( - \infty , \infty ) C) domain: ( - \infty , 0 ] \cup [ 0 , \infty ) ; range: ( - \infty , - 2 ] \cup [ - 2 , \infty ) D) domain: ( - \infty , 0 ) \cup ( 0 , \infty ) ; range: ( - \infty , - 2 ) \cup ( - 2 , \infty )


A) domain: (−∞,−2) ∪(−2,∞) ( - \infty , - 2 ) \cup ( - 2 , \infty ) ; range: (−∞,0) ∪(0,∞) ( - \infty , 0 ) \cup ( 0 , \infty )
B) domain: (−∞,∞) ( - \infty , \infty ) ; range: (−∞,∞) ( - \infty , \infty )
C) domain: (−∞,0]∪[0,∞) ( - \infty , 0 ] \cup [ 0 , \infty ) ; range: (−∞,−2]∪[−2,∞) ( - \infty , - 2 ] \cup [ - 2 , \infty )
D) domain: (−∞,0) ∪(0,∞) ( - \infty , 0 ) \cup ( 0 , \infty ) ; range: (−∞,−2) ∪(−2,∞) ( - \infty , - 2 ) \cup ( - 2 , \infty )

E) A) and B)
F) A) and C)

Correct Answer

verifed

verified

The graph of y = f(x) is given. Use the graph to find the function value. -The graph of y = f(x) is given. Use the graph to find the function value. -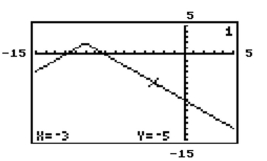 Find f(-3) . A) -3 B) 2 C) -5 D) None of these Find f(-3) .


A) -3
B) 2
C) -5
D) None of these

E) C) and D)
F) All of the above

Correct Answer

verifed

verified

Showing 121 - 140 of 522

Related Exams

Exam 1

Review of Basic Concepts

639 Questions

Exam 2

Equations and Inequalities

496 Questions

Exam 4

Polynomial and Rational Functions

508 Questions

Exam 5

Inverse, Exponential, and Logarithmic Functions

472 Questions

Exam 6

Trigonometric Functions

297 Questions

Exam 7

The Circular Functions and Their Graphs

286 Questions

Exam 8

Trigonometric Identities and Equations

492 Questions

Exam 9

Applications of Trigonometry

447 Questions

Exam 10

Systems and Matrices

507 Questions

Exam 11

Analytic Geometry

217 Questions

Exam 12

Further Topics in Algebra

348 Questions

Show Answer