Filters
Question type
Study Flashcards

Identify and graph the polar equation. - r=4θr=4 \theta Identify and graph the polar equation. - r=4 \theta A) logarithmic spiral B) logarithmic spiral C) logarithmic spiral D) logarithmic spiral


A)
Identify and graph the polar equation. - r=4 \theta A) logarithmic spiral B) logarithmic spiral C) logarithmic spiral D) logarithmic spiral
logarithmic spiral

B)
Identify and graph the polar equation. - r=4 \theta A) logarithmic spiral B) logarithmic spiral C) logarithmic spiral D) logarithmic spiral
logarithmic spiral
C)
Identify and graph the polar equation. - r=4 \theta A) logarithmic spiral B) logarithmic spiral C) logarithmic spiral D) logarithmic spiral
logarithmic spiral

D)
Identify and graph the polar equation. - r=4 \theta A) logarithmic spiral B) logarithmic spiral C) logarithmic spiral D) logarithmic spiral
logarithmic spiral

E) A) and B)
F) A) and C)

Correct Answer

verifed

verified

Write the vector v in the form ai + bj, given its magnitude v and the angle  it makes with the positive x-axis. - ∥v∥=14,α=0∘\| \mathbf { v } \| = 14 , \quad \alpha = 0 ^ { \circ }


A) v=14iv = 14 \mathbf { i }
B) v=14i+14jv = 14 i + 14 j
C) v=14j\mathbf { v } = 14 \mathbf { j }
D) v=−14j\mathbf { v } = - 14 \mathrm { j }

E) C) and D)
F) B) and C)

Correct Answer

verifed

verified

Use the given vectors to find the indicated expression. - v=2i+2j+2k,w=−4i−3j+4k,u=5i+2j+5k\mathbf { v } = 2 \mathbf { i } + 2 \mathbf { j } + 2 \mathbf { k } , \quad \mathbf { w } = - 4 \mathbf { i } - 3 \mathbf { j } + 4 \mathbf { k } , \quad \mathbf { u } = 5 \mathbf { i } + 2 \mathbf { j } + 5 \mathbf { k } Find u⋅(v×w) \mathbf { u } \cdot ( \mathbf { v } \times \mathbf { w } ) .


A) 48
B) 24
C) 58
D) −24- 24

E) A) and B)
F) A) and C)

Correct Answer

verifed

verified

Test the equation for symmetry with respect to the given axis, line, or pole. - r=3+3cos⁡θ;r = 3 + 3 \cos \theta ; the line θ=π2\theta = \frac { \pi } { 2 }


A) Symmetric with respect to the line θ=π2\theta = \frac { \pi } { 2 }
B) May or may not be symmetric with respect to the line θ=π2\theta = \frac { \pi } { 2 }

C) A) and B)
D) undefined

Correct Answer

verifed

verified

Find the unit vector having the same direction as v. - v=−12i+5j\mathbf { v } = - 12 \mathbf { i } + 5 \mathbf { j }


A) u=−1213i+513j\mathbf { u } = - \frac { 12 } { 13 } \mathbf { i } + \frac { 5 } { 13 } \mathbf { j }
B) u=−1312i+135j\mathbf { u } = - \frac { 13 } { 12 } \mathbf { i } + \frac { 13 } { 5 } \mathbf { j }
C) u=−513i+1213j\mathbf { u } = - \frac { 5 } { 13 } \mathbf { i } + \frac { 12 } { 13 } \mathbf { j }
D) u=−156i+65j\mathbf { u } = - 156 \mathbf { i } + 65 \mathbf { j }

E) B) and D)
F) B) and C)

Correct Answer

verifed

verified

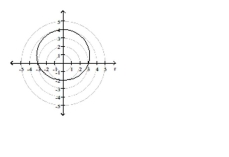
Match the graph to one of the polar equations. - Match the graph to one of the polar equations. - A) r = 3 + \sin \theta B) r = 6 \sin \theta C) r = 3 + \cos \theta D) r = 6 \cos \theta


A) r=3+sin⁡θr = 3 + \sin \theta
B) r=6sin⁡θr = 6 \sin \theta
C) r=3+cos⁡θr = 3 + \cos \theta
D) r=6cos⁡θr = 6 \cos \theta

E) None of the above
F) All of the above

Correct Answer

verifed

verified

Find the position vector for the vector having initial point P and terminal point Q. - P=(0,0,0) \mathrm { P } = ( 0,0,0 ) and Q=(−3,3,4) \mathrm { Q } = ( - 3,3,4 )


A) v=−3i+3j+4k\mathbf { v } = - 3 \mathrm { i } + 3 \mathrm { j } + 4 \mathbf { k }
B) v=−3i+3j−4kv = - 3 i + 3 j - 4 k
C) v=4i+3j−3k\mathbf { v } = 4 \mathbf { i } + 3 \mathbf { j } - 3 \mathbf { k }
D) v=3i−3j−4k\mathbf { v } = 3 \mathbf { i } - 3 \mathbf { j } - 4 \mathbf { k }

E) B) and C)
F) A) and C)

Correct Answer

verifed

verified

Write the vector v in the form ai + bj, given its magnitude v and the angle  it makes with the positive x-axis. - ∥v∥=15,α=45∘\| \mathbf { v } \| = 15 , \alpha = 45 ^ { \circ }


A) v=15(1532i+152j) \mathbf { v } = 15 \left( \frac { 15 \sqrt { 3 } } { 2 } \mathbf { i } + \frac { 15 } { 2 } \mathbf { j } \right)
B) v=15(152i+1532j) \mathbf { v } = 15 \left( \frac { 15 } { 2 } \mathrm { i } + \frac { 15 \sqrt { 3 } } { 2 } \mathrm { j } \right)
C) v=15(−22i−22j) v = 15 \left( - \frac { \sqrt { 2 } } { 2 } i - \frac { \sqrt { 2 } } { 2 } j \right)
D) v=15(22i+22j) \mathbf { v } = 15 \left( \frac { \sqrt { 2 } } { 2 } \mathrm { i } + \frac { \sqrt { 2 } } { 2 } \mathrm { j } \right)

E) All of the above
F) A) and B)

Correct Answer

verifed

verified

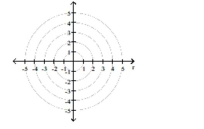
Graph the polar equation. - r=51−5sin⁡θr=\frac{5}{1-5 \sin \theta} Graph the polar equation. - r=\frac{5}{1-5 \sin \theta} A) B) C) D)


A)
Graph the polar equation. - r=\frac{5}{1-5 \sin \theta} A) B) C) D)

B)
Graph the polar equation. - r=\frac{5}{1-5 \sin \theta} A) B) C) D)
C)
Graph the polar equation. - r=\frac{5}{1-5 \sin \theta} A) B) C) D)

D)
Graph the polar equation. - r=\frac{5}{1-5 \sin \theta} A) B) C) D)

E) B) and C)
F) None of the above

Correct Answer

verifed

verified

Write the vector v in the form ai + bj, given its magnitude v and the angle  it makes with the positive x-axis. - ∥v∥=7,α=270∘\| v \| = 7 , \alpha = 270 ^ { \circ }


A) v=−7i\mathbf { v } = - 7 \mathbf { i }
B) v=−7i+7j) \mathbf { v } = - 7 \mathrm { i } + 7 \mathrm { j } )
C) v=−7i−7j\mathbf { v } = - 7 \mathbf { i } - 7 \mathbf { j }
D) v=−7j\mathbf { v } = - 7 \mathrm { j }

E) A) and B)
F) B) and D)

Correct Answer

verifed

verified

Find all the complex roots. Leave your answers in polar form with the argument in degrees. -The complex fifth roots of 3+i\sqrt { 3 } + i


A) 25(cos⁡30∘+isin⁡30∘) ,25(cos⁡102∘+isin⁡102∘) ,25(cos⁡174∘+isin⁡174∘) ,25(cos⁡246∘+isin⁡246∘) \sqrt [ 5 ] { 2 } \left( \cos 30 ^ { \circ } + i \sin 30 ^ { \circ } \right) , \sqrt [ 5 ] { 2 } \left( \cos 102 ^ { \circ } + i \sin 102 ^ { \circ } \right) , \sqrt [ 5 ] { 2 } \left( \cos 174 ^ { \circ } + i \sin 174 ^ { \circ } \right) , \sqrt [ 5 ] { 2 } \left( \cos 246 ^ { \circ } + i \sin 246 ^ { \circ } \right) , 25(cos⁡318∘+isin⁡318∘) \sqrt [ 5 ] { 2 } \left( \cos 318 ^ { \circ } + i \sin 318 ^ { \circ } \right)
B) 32(cos⁡6∘+isin⁡6∘) ,32(cos⁡78∘+isin⁡78∘) ,32(cos⁡150∘+isin⁡150∘) ,32(cos⁡222∘+isin⁡222∘) 32 \left( \cos 6 ^ { \circ } + i \sin 6 ^ { \circ } \right) , 32 \left( \cos 78 ^ { \circ } + i \sin 78 ^ { \circ } \right) , 32 \left( \cos 150 ^ { \circ } + i \sin 150 ^ { \circ } \right) , 32 \left( \cos 222 ^ { \circ } + i \sin 222 ^ { \circ } \right) , 32(cos⁡294∘+isin⁡294∘) 32 \left( \cos 294 ^ { \circ } + \mathrm { i } \sin 294 ^ { \circ } \right)
C) 32(cos⁡30∘+isin⁡30∘) ,32(cos⁡102∘+isin⁡102∘) ,32(cos⁡174∘+isin⁡174∘) ,32(cos⁡246∘+isin⁡246∘) 32 \left( \cos 30 ^ { \circ } + i \sin 30 ^ { \circ } \right) , 32 \left( \cos 102 ^ { \circ } + i \sin 102 ^ { \circ } \right) , 32 \left( \cos 174 ^ { \circ } + i \sin 174 ^ { \circ } \right) , 32 \left( \cos 246 ^ { \circ } + i \sin 246 ^ { \circ } \right) , 32(cos⁡318∘+isin⁡318∘) 32 \left( \cos 318 ^ { \circ } + i \sin 318 ^ { \circ } \right)

D) 25(cos⁡6∘+isin⁡6∘) ,25(cos⁡78∘+isin⁡78∘) ,25(cos⁡150∘+isin⁡150∘) ,25(cos⁡222∘+isin⁡222∘) \sqrt [ 5 ] { 2 } \left( \cos 6 ^ { \circ } + i \sin 6 ^ { \circ } \right) , \sqrt [ 5 ] { 2 } \left( \cos 78 ^ { \circ } + i \sin 78 ^ { \circ } \right) , \sqrt [ 5 ] { 2 } \left( \cos 150 ^ { \circ } + i \sin 150 ^ { \circ } \right) , \sqrt [ 5 ] { 2 } \left( \cos 222 ^ { \circ } + i \sin 222 ^ { \circ } \right) , 25(cos⁡294∘+isin⁡294∘) \sqrt [ 5 ] { 2 } \left( \cos 294 ^ { \circ } + i \sin 294 ^ { \circ } \right)

E) C) and D)
F) None of the above

Correct Answer

verifed

verified

Decompose v into two vectors v1 and v2, where v1 is parallel to w and v2 is orthogonal to w. - v=i+5j,w=i+j\mathbf { v } = \mathrm { i } + 5 \mathrm { j } , \quad \mathbf { w } = \mathrm { i } + \mathrm { j }


A) v1=72i+72j,v2=−52i+32j\mathbf { v } _ { 1 } = \frac { 7 } { 2 } \mathrm { i } + \frac { 7 } { 2 } \mathrm { j } , \mathrm { v } _ { 2 } = - \frac { 5 } { 2 } \mathrm { i } + \frac { 3 } { 2 } \mathrm { j }
B) v1=3i+3j) ,v2=−2i+2j\left. \mathbf { v } _ { 1 } = 3 \mathbf { i } + 3 \mathbf { j } \right) , \mathbf { v } _ { 2 } = - 2 \mathbf { i } + 2 \mathbf { j }
C) v1=6i+6j,v2=−4i+4j\mathbf { v } _ { 1 } = 6 \mathbf { i } + 6 \mathbf { j } , \mathbf { v } _ { 2 } = - 4 \mathbf { i } + 4 \mathbf { j }
D) v1=3i+3j,v2=2i−2j\mathbf { v } _ { 1 } = 3 \mathbf { i } + 3 \mathbf { j } , \mathbf { v } _ { 2 } = 2 \mathbf { i } - 2 \mathbf { j }

E) A) and D)
F) B) and C)

Correct Answer

verifed

verified

Solve the problem. -If v=3i+4j\mathbf { v } = 3 \mathbf { i } + 4 \mathbf { j } , find ∥v∥\| \mathbf { v } \| .


A) 5
B) 7
C) 5\sqrt { 5 }
D) 25

E) A) and B)
F) A) and C)

Correct Answer

verifed

verified

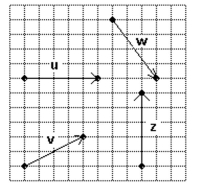Use the vectors in the figure below to graph the following vector. Use the vectors in the figure below to graph the following vector. - \mathbf { u } + \mathrm { z } A) B) C) D) - u+z\mathbf { u } + \mathrm { z } Use the vectors in the figure below to graph the following vector. - \mathbf { u } + \mathrm { z } A) B) C) D)


A)
Use the vectors in the figure below to graph the following vector. - \mathbf { u } + \mathrm { z } A) B) C) D)

B)
Use the vectors in the figure below to graph the following vector. - \mathbf { u } + \mathrm { z } A) B) C) D)

C)
Use the vectors in the figure below to graph the following vector. - \mathbf { u } + \mathrm { z } A) B) C) D)

D)
Use the vectors in the figure below to graph the following vector. - \mathbf { u } + \mathrm { z } A) B) C) D)

E) B) and C)
F) C) and D)

Correct Answer

verifed

verified

Find the dot product v · w. - v=i+j\mathbf { v } = \mathrm { i } + \mathrm { j } and w=i+j−k\mathbf { w } = \mathrm { i } + \mathrm { j } - \mathbf { k }


A) 1
B) 3
C) −2- 2
D) 2

E) A) and B)
F) None of the above

Correct Answer

verifed

verified

Solve the problem. Leave your answer in polar form. - z=2+2iw=3−i\begin{array} { l } z = 2 + 2 i \\w = \sqrt { 3 } - i\end{array} Find zw.


A) 42(cos⁡23π12+isin⁡23π12) 4 \sqrt { 2 } \left( \cos \frac { 23 \pi } { 12 } + i \sin \frac { 23 \pi } { 12 } \right)
B) 4(cos⁡π12+isin⁡π12) 4 \left( \cos \frac { \pi } { 12 } + i \sin \frac { \pi } { 12 } \right)
C) 4(cos⁡23π12+isin⁡23π12) 4 \left( \cos \frac { 23 \pi } { 12 } + i \sin \frac { 23 \pi } { 12 } \right)
D) 42(cos⁡π12+isin⁡π12) 4 \sqrt { 2 } \left( \cos \frac { \pi } { 12 } + i \sin \frac { \pi } { 12 } \right)

E) A) and C)
F) B) and C)

Correct Answer

verifed

verified

Use the given vectors to find the indicated expression. - v=−4i−3j+2k,w=−5i−5j+4k,u=4i+4j−4k\mathbf { v } = - 4 \mathbf { i } - 3 \mathbf { j } + 2 \mathbf { k } , \quad \mathbf { w } = - 5 \mathbf { i } - 5 \mathbf { j } + 4 \mathbf { k } , \quad \mathbf { u } = 4 \mathbf { i } + 4 \mathbf { j } - 4 \mathbf { k } Find w⋅(v×u) \mathbf { w } \cdot ( \mathbf { v } \times \mathbf { u } ) .


A) 148
B) 4
C) 172
D) 0

E) A) and B)
F) A) and C)

Correct Answer

verifed

verified

Find the angle between v and w. Round to one decimal place, if necessary. - v=i+j\mathbf { v } = \mathrm { i } + \mathrm { j } and w=i+j−k\mathbf { w } = \mathrm { i } + \mathbf { j } - \mathbf { k }


A) 66∘66 ^ { \circ }
B) 0∘0 ^ { \circ }
C) 35.3∘35.3 ^ { \circ }
D) 90∘90 ^ { \circ }

E) None of the above
F) B) and D)

Correct Answer

verifed

verified

Choose the one alternative that best completes the statement or answers the question. Find the direction angles of the vector. Round to the nearest degree, if necessary. - v=−2i+3j−4k\mathbf { v } = - 2 \mathbf { i } + 3 \mathbf { j } - 4 \mathbf { k }


A) α=119∘,β=43∘,γ=166∘\alpha = 119 ^ { \circ } , \beta = 43 ^ { \circ } , \gamma = 166 ^ { \circ }
B) α=115∘,β=51∘,γ=147∘\alpha = 115 ^ { \circ } , \beta = 51 ^ { \circ } , \gamma = 147 ^ { \circ }
C) α=112∘,β=124∘,γ=138∘\alpha = 112 ^ { \circ } , \beta = 124 ^ { \circ } , \gamma = 138 ^ { \circ }
D) α=113∘,β=55∘,γ=140∘\alpha = 113 ^ { \circ } , \beta = 55 ^ { \circ } , \gamma = 140 ^ { \circ }

E) B) and D)
F) B) and C)

Correct Answer

verifed

verified

Write the vector v in the form ai + bj, given its magnitude v and the angle  it makes with the positive x-axis. - ∥v∥=7,α=60∘\| \mathbf { v } \| = 7 , \quad \alpha = 60 ^ { \circ }


A) v=7(−72i−732j) v = 7 \left( - \frac { 7 } { 2 } i - \frac { 7 \sqrt { 3 } } { 2 } j \right)
B) v=7(732i+72j) v = 7 \left( \frac { 7 \sqrt { 3 } } { 2 } \mathrm { i } + \frac { 7 } { 2 } \mathrm { j } \right)
C) v=7(22i+22j) v = 7 \left( \frac { \sqrt { 2 } } { 2 } \mathrm { i } + \frac { \sqrt { 2 } } { 2 } \mathrm { j } \right)
D) v=7(72i+732j) v = 7 \left( \frac { 7 } { 2 } \mathrm { i } + \frac { 7 \sqrt { 3 } } { 2 } \mathrm { j } \right)

E) A) and D)
F) B) and C)

Correct Answer

verifed

verified

Showing 121 - 140 of 253

Related Exams

Exam 1

Functions and Their Graphs

297 Questions

Exam 2

Linear and Quadratic Functions

302 Questions

Exam 3

Polynomial and Rational Functions

354 Questions

Exam 4

Exponential and Logarithmic Functions

517 Questions

Exam 5

Trigonometric Functions

354 Questions

Exam 6

Analytic Trigonometry

342 Questions

Exam 7

Applications of Trigonometric Functions

105 Questions

Exam 9

Analytic Geometry

200 Questions

Exam 10

Systems of Equations and Inequalities

235 Questions

Exam 11

Sequences; Induction; the Binomial Theorem

238 Questions

Exam 12

Counting and Probability

115 Questions

Exam 13

A Preview of Calculus: the Limit, Derivative, and Integral of a Function

145 Questions

Exam 14

Foundations: a Prelude to Functions

234 Questions

Exam 15

Graphing Utilities

29 Questions

Show Answer