A) 2r sin( ) ![]() + r cos( )
+ r cos( ) ![]() + 2z k
+ 2z k
B) 2r sin( ) ![]() +
+ ![]() cos( )
cos( ) ![]() + 2z k
+ 2z k
C) 2r cos( ) ![]() + r sin( )
+ r sin( ) ![]() + 2z k
+ 2z k
D) 2r cos( ) ![]() +
+ ![]() sin( )
sin( ) ![]() + 2z k
+ 2z k
E) r sin( ) ![]() +
+ ![]() cos( )
cos( ) ![]() + 2z k
+ 2z k
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In spherical coordinates, find 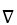 f for f =
f for f = 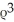 sin( ) cos( ) .
sin( ) cos( ) .
A) 3 ![]() sin( ) cos( )
sin( ) cos( ) ![]() +
+ ![]() cos( ) cos( )
cos( ) cos( ) ![]() -
- ![]() sin( )
sin( ) ![]()
B) 3 ![]() sin( ) cos( )
sin( ) cos( ) ![]() +
+ ![]() cos( ) cos( )
cos( ) cos( ) ![]() -
- ![]() sin( ) sin( )
sin( ) sin( ) ![]()
C) ![]()
D) 3 ![]() sin( ) cos( )
sin( ) cos( ) ![]() -
- ![]() cos( ) cos( )
cos( ) cos( ) ![]() +
+ ![]() sin( )
sin( ) ![]()
E) 3 ![]() sin( ) cos( )
sin( ) cos( ) ![]() -
- ![]() cos( ) cos( )
cos( ) cos( ) ![]() -
- ![]() sin( )
sin( ) ![]()
G) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In cylindrical coordinates, find 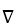 . F for F =
. F for F = 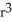
 + rz cos( )
+ rz cos( )  + rz sin( ) k.
+ rz sin( ) k.
A) 4 ![]() - z sin( ) + sin( )
- z sin( ) + sin( )
B) 4 ![]() - z sin( ) + r sin( )
- z sin( ) + r sin( )
C) 3 ![]() - sin( ) + r sin( )
- sin( ) + r sin( )
D) 3 ![]() - z sin( ) - r sin( )
- z sin( ) - r sin( )
E) 3 ![]() - z sin( ) + sin( )
- z sin( ) + sin( )
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use Green's theorem in the plane to find the x-coordinate of the centroid of a regular plane region R (with areaA) enclosed by a positively oriented, piecewise smooth, simple closed curve C .
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let F = - 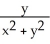 i +
i + 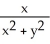 j and let C be the boundary of circle
j and let C be the boundary of circle 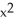 +
+ 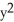 = 9 oriented counterclockwise. Use Green's Theorem to evaluate
= 9 oriented counterclockwise. Use Green's Theorem to evaluate 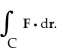
A) 9
B) 0
C) -2
D) 2
E) 3
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Using spherical polar coordinates, find 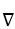 × F for F =
× F for F = 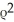 sin( )
sin( )  + sin( )
+ sin( ) 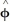 +
+ 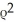 cos( )
cos( )  .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If r = x i + y j + z k and k is a constant vector field in R3, then
A) div ( k × r) = 0
B) div ( k × r) = 0.
C) grad ( k . r) = 2k
D) curl ( k × r) = 0
E) curl ( k × r) = 0.
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate 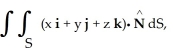 where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
A) ![]()
![]()
B) ![]()
C) ![]()
![]()
D) 2 ![]()
E) ![]()
![]()
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use Green's Theorem to compute the integral 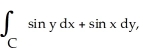 where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
A) 3
B) 2
C) 1
D) 0
E)
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find all values of the nonzero constant real numbers a, b, and c so that the vector field F = a cos( 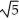 x + 2y ) cosh (c z) i + b cos (
x + 2y ) cosh (c z) i + b cos ( 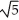 x + 2y) cosh (c z) j + c sin(
x + 2y) cosh (c z) j + c sin( 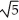 x + 2y) sinh(c z) k is both and .
x + 2y) sinh(c z) k is both and .
A) a = - ![]() , b = -2, c = 3
, b = -2, c = 3
B) a = ![]() , b = 2, c = 2
, b = 2, c = 2
C) a = - ![]() , b = -2, c =
, b = -2, c = ![]() ± 2
± 2
D) a = ![]() , b = 2, c = ± 3
, b = 2, c = ± 3
E) a = ![]() , b = -2, c = 9
, b = -2, c = 9
G) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use Stokes's Theorem to evaluate the integral 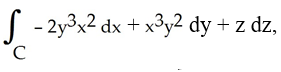 where C is the curve of intersection of the sphere
where C is the curve of intersection of the sphere 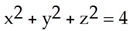 and the plane
and the plane 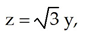 oriented counterclockwise as seen from high on the z-axis.
oriented counterclockwise as seen from high on the z-axis.
A) 2
B) 3
C) 4
D) 5
E) 0
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If C is the positively oriented boundary of a plane region R having area 3 units and centroid at the point (12, 6) , evaluate (i) 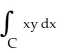 (ii)
(ii) 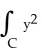 dx + 3xy dy
dx + 3xy dy
A) (i) 36 (ii) 15
B) (i) -36 (ii) 18
C) (i) -18 (ii) 36
D) (i) -4 (ii) 2
E) (i) 432 (ii) 1080
G) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use Stokes's Theorem to evaluate the line integral 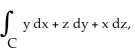 where C is the triangle with vertices (0, 0, 1) , (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
where C is the triangle with vertices (0, 0, 1) , (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
A) 0
B) 1
C) -1
D) 2
E) -2
G) D) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let 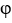 and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity
and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity 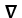 . (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
. (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
A) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
B) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = curl (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 grad (F)
C) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
D) grad (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 curl (F)
E) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_d4f5_2c01_ae82_0ffef783bd40_TB9661_11 grad (F)
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate 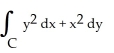 clockwise around the triangle with vertices (0, 0) , (3, 0) , and (3, 3) .
clockwise around the triangle with vertices (0, 0) , (3, 0) , and (3, 3) .
A) 27
B) 9
C) -9
D) -27
E) 0
G) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Define the curl of a vector field F.
A) F × ![]()
B) ![]() F
F
C) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 × F
D) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 . F
E) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 F
G) D) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the flux of 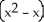 i - xy j +3z k out of the solid region bounded by the parabolic cylinder
i - xy j +3z k out of the solid region bounded by the parabolic cylinder 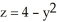 and the planes
and the planes 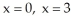 , and
, and 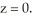
A) 208
B) 112
C) 64
D) 48
E) 176
G) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the integral 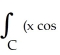 (
( 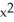 ) - 2y) dx + (3x - ysin(
) - 2y) dx + (3x - ysin( 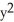 ) ) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0) , (2, 2) , and (2, 0) .
) ) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0) , (2, 2) , and (2, 0) .
A) 5
B) 20
C) 0
D) 10
E) 2
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let F be a smooth vector field in 3-space satisfying the condition 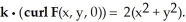 Find the flux of curl F upward through the part of the
Find the flux of curl F upward through the part of the 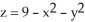 lying above the xy-plane.
lying above the xy-plane.
A) 81
B) 72
C) 27
D) 18
E) None of the above
G) C) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A vector field F is called in a domain D if
A) ![]() F = 0 in D
F = 0 in D
B) curl(F) = 0 in D
C) F = ![]()
![]() in D for some scalar field 11ee7bad_3b7e_852d_ae82_0ffea7b87591_TB9661_11
in D for some scalar field 11ee7bad_3b7e_852d_ae82_0ffea7b87591_TB9661_11
D) div(F) = 0 in D
E) grad(F) = 0 in D
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Showing 21 - 40 of 92
Related Exams