A)
B)
C)
D)
E)
G) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Give the coordinates of the circle's center and its radius.
A) (1,1) ;r = 64
B) (0,0) ;r = 8
C) (1,1) ;r = 8
D) (0,0) ;r = 64
E) none of these
G) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex and directrix of the parabola.
A) vertex: directrix: y=1
B) vertex: directrix: y=12
C) vertex: directrix: y=6
D) vertex: directrix: y=-1
E) vertex: directrix: y=-7
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center and vertices of the hyperbola and sketch its graph,using asymptotes as sketching aids.
A) Center: (0,0) Vertices: (-5,0) ![]()
B) Center: (0,0) Vertices: (-3,0) ![]()
C) Center: (0,0) Vertices: (3,0) ![]()
D) Center: (0,0) Vertices: (±5,0) ![]()
E) Center: (0,0) Vertices: (±3,0) ![]()
G) B) and C)
Correct Answer

verified
E
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Focus:
A)
B)
C)
D)
E)
G) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Give the standard form of the equation of the parabola with the given characteristics. vertex: (-7,-2) focus: (-5,-2)
A)
B)
C)
D)
E)
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex,focus,and directrix of the parabola.
A) Vertex: (0,0) ;Focus: ;Directrix:
B) Vertex:(0,0) ;Focus: ;Directrix:
C) Vertex: (0,0) ;Focus: ;Directrix:
D) Vertex: (0,0) ;Focus: ;Directrix:
E) Vertex: (0,0) ;Focus: ;Directrix:
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex and focus of the parabola from the given equation and select its graph.
A) Vertex: (0,0) Focus: (0,-1.5) ![]()
B) Vertex: (0,0) Focus: (-1.5,0) ![]()
C) Vertex: (0,0) Focus: (0,1.5) ![]()
D) Vertex: (0,0) Focus: (0,1.5) ![]()
E) Vertex: (0,0) Focus: (0,-1.5) ![]()
G) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The equations of a parabola and a tangent line to the parabola are given.Select the correct graph of both equations in the same viewing window. Parabola: Tangent Line:
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Horizontal axis and passes through the point
A)
B)
C)
D)
E)
G) B) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. Focies: (±7,0) ;major axis of length 16
A)
B)
C)
D)
E)
G) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the parabola so that its graph matches the description. ;lower half of parabola
A)
B)
C)
D)
E)
G) C) and D)
Correct Answer

verified
B
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the hyperbola with the given characteristics. focies: (±4,0) ,asymptotes:
A)
B)
C)
D)
E)
G) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Horizontal axis and passes through the point
A)
B)
C)
D)
E)
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the parabola so that its graph matches the description. ;upper half of parabola
A)
B)
C)
D)
E)
G) B) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Select the graph of the following equation:
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) C) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex,focus,and directrix of the parabola.
A) Vertex: ;Focus: ;Directrix:
B) Vertex: ;Focus: ;Directrix:
C) Vertex: ;Focus: ;Directrix:
D) Vertex: ;Focus: ;Directrix:
E) Vertex: ;Focus: ;Directrix:
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex,focus,and directrix of the parabola.
A) Vertex: (0,0) ;Focus: ;Directrix:
B) Vertex: (0,0) ;Focus: ;Directrix:
C) Vertex: (0,0) ;Focus: ;Directrix:
D) Vertex: (0,0) ;Focus: ;Directrix:
E) Vertex: (0,0) ;Focus: ;Directrix:
G) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the parabola and determine the coordinates of the focus. 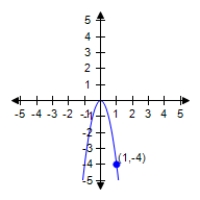
A) ,focus:
B) ,focus:
C) ,focus:
D) ,focus: (0,-4)
E) ,focus:
G) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The receiver in a parabolic satellite dish is 4.5 feet from the vertex and is located at the focus (see figure) .Write an equation for a cross section of the reflector.(Assume that the dish is directed upward and the vertex is at the origin. ) 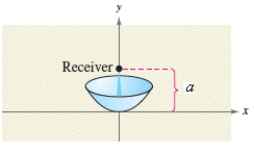
A)
B)
C)
D)
E)
G) A) and B)
Correct Answer

verified
D
Correct Answer
verified
Showing 1 - 20 of 124
Related Exams