Question 1

Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin. ​
Vertices: (±3,0) ;passes through the point ​  (5,3) ( 5 , \sqrt { 3 } ) (5,3​)   ​

Accepted Answer

A)    y29−x227/16=−1\frac { y ^ { 2 } } { 9 } - \frac { x ^ { 2 } } { 27 / 16 } = - 19y2​−27/16x2​=−1 
B)    x227/16+y29=1\frac { x ^ { 2 } } { 27 / 16 } + \frac { y ^ { 2 } } { 9 } = 127/16x2​+9y2​=1 
C)    x29−y227/16=1\frac { x ^ { 2 } } { 9 } - \frac { y ^ { 2 } } { 27 / 16 } = 19x2​−27/16y2​=1 
D)    x227/16+y29=−1\frac { x ^ { 2 } } { 27 / 16 } + \frac { y ^ { 2 } } { 9 } = - 127/16x2​+9y2​=−1 
E)    y29+x227/16=1\frac { y ^ { 2 } } { 9 } + \frac { x ^ { 2 } } { 27 / 16 } = 19y2​+27/16x2​=1F) B) and E)
G) B) and D)

Question 2

Find the vertex and focus of the parabola from the given equation and select its graph.​  2x+y2=02 x + y ^ { 2 } = 02x+y2=0  ​

Accepted Answer

A)  Vertex: (0,0)  Focus: (-  12\frac { 1 } { 2 }21​  ,0)  
B)  Vertex: (-  12\frac { 1 } { 2 }21​  ,0)  Focus: (0,0)  
C)  Vertex: (0,0)  Focus: (0,  12\frac { 1 } { 2 }21​  )  
D)  Vertex: (0,0)  Focus: (0,-  12\frac { 1 } { 2 }21​  )  
E)  Vertex: (0,0)  Focus: (  12\frac { 1 } { 2 }21​  ,0)   F) A) and D)
G) All of the above

Question 3

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. focus: (0,-2)

Accepted Answer

A)  y2 = -8x
B)  x2 = -8y
C)  x2 = -2y
D)  y2 = -2x
E)  x2 = 2yF) C) and D)
G) B) and D)

Question 4

Find the vertex and directrix of the parabola.  x2−14x−8y+73=0x ^ { 2 } - 14 x - 8 y + 73 = 0x2−14x−8y+73=0

Accepted Answer

A)  vertex:  (7,3) ( 7,3 ) (7,3)   directrix:  y=5y = 5y=5 
B)  vertex:  (−7,−3) ( - 7 , - 3 ) (−7,−3)   directrix:  y=5y = 5y=5 
C)  vertex:  (7,3) ( 7,3 ) (7,3)   directrix:  y=1y = 1y=1 
D)  vertex:  (−7,−3) ( - 7 , - 3 ) (−7,−3)   directrix:  y=−5y = - 5y=−5 
E)  vertex:  (−7,−3) ( - 7 , - 3 ) (−7,−3)   directrix:  y=9y = 9y=9F) A) and E)
G) B) and E)

Question 5

Find the standard form of the equation of the parabola with the given characteristics. ​
Vertex:  (0,2) ( 0,2 ) (0,2)   ;directrix:  y=10y = 10y=10  ​

Accepted Answer

A)    x2=−32(y−10) x ^ { 2 } = - 32 ( y - 10 ) x2=−32(y−10)  
B)    y2=−32(x−2) y ^ { 2 } = - 32 ( x - 2 ) y2=−32(x−2)  
C)    x2=32(y−2) x ^ { 2 } = 32 ( y - 2 ) x2=32(y−2)  
D)    y2=32(x−2) y ^ { 2 } = 32 ( x - 2 ) y2=32(x−2)  
E)    x2=−32(y−2) x ^ { 2 } = - 32 ( y - 2 ) x2=−32(y−2) F) A) and C)
G) A) and B)

Question 6

Find the vertex,focus,and directrix of the parabola.​  y2=−3xy ^ { 2 } = - 3 xy2=−3x  ​

Accepted Answer

A)  Vertex: (0,0) ;Focus:  (−34,0) \left( - \frac { 3 } { 4 } , 0 \right) (−43​,0)   ;Directrix:  x=−34x = - \frac { 3 } { 4 }x=−43​ 
B)  Vertex: (0,0) ;Focus:  (−13,0) \left( - \frac { 1 } { 3 } , 0 \right) (−31​,0)   ;Directrix:  x=13x = \frac { 1 } { 3 }x=31​ 
C)  Vertex: (0,0) ;Focus:  (13,0) \left( \frac { 1 } { 3 } , 0 \right) (31​,0)   ;Directrix:  x=13x = \frac { 1 } { 3 }x=31​ 
D)  Vertex: (0,0) ;Focus:  (34,0) \left( \frac { 3 } { 4 } , 0 \right) (43​,0)   ;Directrix:  x=−34x = - \frac { 3 } { 4 }x=−43​ 
E)  Vertex: (0,0) ;Focus:  (−34,0) \left( - \frac { 3 } { 4 } , 0 \right) (−43​,0)   ;Directrix:  x=34x = \frac { 3 } { 4 }x=43​F) C) and D)
G) B) and E)

Question 7

As a speeding train crosses a trestle over a deep gorge,a child drops his toy plane from the window.The path of the toy plane is modeled by  x2=−7.0(y−185) x ^ { 2 } = - 7.0 ( y - 185 ) x2=−7.0(y−185)   ,where y is the height above the floor of the gorge and distances are measured in feet.How far will the toy plane travel horizontally before it hits the bottom of the gorge? [Note: The toy plane does not glide;it "drops like a rock."]

Accepted Answer

A)  7.0 ft
B)  36.0 ft
C)  185 ft
D)  1295.0 ft
E)  14 ft F) C) and D)
G) A) and B)

Question 8

Write an equation for a cross section of the parabolic ear (used to hear sounds from a distance) shown in the picture. 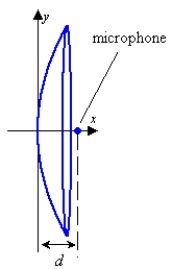 ​ d = 2.25 inches

Accepted Answer

A)    x2=9yx ^ { 2 } = 9 yx2=9y 
B)  ​  y2=19xy ^ { 2 } = \frac { 1 } { 9 } xy2=91​x 
C)  ​  x2=2.25yx ^ { 2 } = 2.25 yx2=2.25y 
D)  ​  y2=2.25xy ^ { 2 } = 2.25 xy2=2.25x 
E)    y2=9xy ^ { 2 } = 9 xy2=9xF) A) and D)
G) C) and E)

Question 9

Identify the conic.​  4y2−8x=04 y ^ { 2 } - 8 x = 04y2−8x=0  ​

Accepted Answer

A)  Circle
B)  Ellipse
C)  Parabola
D)  Hyperbola
E)  Line F) A) and B)
G) B) and E)

Question 10

Find the center and vertices which located on the major axis of the ellipse.  x225+y29=1\frac { x ^ { 2 } } { 25 } + \frac { y ^ { 2 } } { 9 } = 125x2​+9y2​=1

Accepted Answer

A)  center: (0,0) vertices: (0,-5) , (0,5) 
B)  center: (0,0) vertices: (-3,0) , (3,0) 
C)  center: (5,3) vertices: (-5,-3) , (5,3) 
D)  center: (0,0) vertices: (-5,0) , (5,0) 
E)  center: (5,0) vertices: (0,-3) , (0,3)  F) A) and E)
G) C) and E)

Question 11

Find the standard form of the equation of the parabola with the given characteristics. ​
Vertex:  (−5,5) ( - 5,5 ) (−5,5)   ;focus:  (−5,0) ( - 5,0 ) (−5,0)   ​

Accepted Answer

A)    (x−5) 2=20(y−5) ( x - 5 )  ^ { 2 } = 20 ( y - 5 ) (x−5) 2=20(y−5)  
B)    (x−5) 2=−20(y−5) ( x - 5 )  ^ { 2 } = - 20 ( y - 5 ) (x−5) 2=−20(y−5)  
C)    (y−5) 2=−20(x−5) ( y - 5 )  ^ { 2 } = - 20 ( x - 5 ) (y−5) 2=−20(x−5)  
D)    (y−5) 2=20(x−5) ( y - 5 )  ^ { 2 } = 20 ( x - 5 ) (y−5) 2=20(x−5)  
E)    (x+5) 2=−20(y−5) ( x + 5 )  ^ { 2 } = - 20 ( y - 5 ) (x+5) 2=−20(y−5) F) A) and B)
G) C) and E)

Question 12

Find the vertex and focus of the parabola.  x2+8y=0x ^ { 2 } + 8 y = 0x2+8y=0  ​

Accepted Answer

A)  vertex: (0,0) focus: (0,-2) 
B)  vertex: (2,0) focus: (0,0) 
C)  vertex: (0,0) focus: (-2,0) 
D)  vertex: (0,0) focus: (0,2) 
E)  vertex: (-2,0) focus: (0,0)  F) A) and E)
G) B) and C)

Question 13

Find the vertex and focus of the parabola from the given equation and select its graph.​  y2=6xy ^ { 2 } = 6 xy2=6x  ​

Accepted Answer

A)  Vertex: (0,0)  Focus: (-  32\frac { 3 } { 2 }23​  ,0)  
B)  Vertex: (0,0)  Focus: (0,-  32\frac { 3 } { 2 }23​  )  
C)  Vertex: (0,0)  Focus: (  32\frac { 3 } { 2 }23​  ,0)  
D)  Vertex: (0,0)  Focus: (0,  32\frac { 3 } { 2 }23​  )  
E)  Vertex: (0,0)  Focus: (  32\frac { 3 } { 2 }23​  ,0)   F) C) and D)
G) A) and B)

Question 14

Find the vertices and asymptotes of the hyperbola.  25y2−4x2=10025 y ^ { 2 } - 4 x ^ { 2 } = 10025y2−4x2=100

Accepted Answer

A)  vertices: (±2,0) ,asymptote:  y=±52xy = \pm \frac { 5 } { 2 } xy=±25​x 
B)  vertices: (0,±2) ,asymptote:  y=±25xy = \pm \frac { 2 } { 5 } xy=±52​x 
C)  vertices: (±2,0) ,asymptote:  y=±25xy = \pm \frac { 2 } { 5 } xy=±52​x 
D)  vertices: (0,±2) ,asymptote:  y=±52xy = \pm \frac { 5 } { 2 } xy=±25​x 
E)  vertices: (±2,5) ,asymptote:  y=±25xy = \pm \frac { 2 } { 5 } xy=±52​xF) All of the above
G) B) and D)

Question 15

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. ​
Directrix:  y=3y = 3y=3  ​

Accepted Answer

A)    y2=−12xy ^ { 2 } = - 12 xy2=−12x 
B)    y2=xy ^ { 2 } = xy2=x 
C)    y2=12xy ^ { 2 } = 12 xy2=12x 
D)    x2=12yx ^ { 2 } = 12 yx2=12y 
E)    x2=−12yx ^ { 2 } = - 12 yx2=−12yF) None of the above
G) A) and E)

Question 16

Give the standard form of the equation of the parabola with the given characteristics. vertex: (7,8) focus: (5,8)

Accepted Answer

A)    (y+8) 2=−8(x+7) ( y + 8 )  ^ { 2 } = - 8 ( x + 7 ) (y+8) 2=−8(x+7)  
B)    (y−8) 2=−8(x−7) ( y - 8 )  ^ { 2 } = - 8 ( x - 7 ) (y−8) 2=−8(x−7)  
C)    (x+7) 2=8(y+8) ( x + 7 )  ^ { 2 } = 8 ( y + 8 ) (x+7) 2=8(y+8)  
D)    (y−8) 2=8(x−7) ( y - 8 )  ^ { 2 } = 8 ( x - 7 ) (y−8) 2=8(x−7)  
E)    (x−7) 2=8(y−8) ( x - 7 )  ^ { 2 } = 8 ( y - 8 ) (x−7) 2=8(y−8) F) A) and D)
G) C) and D)

Question 17

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. directrix: x = -9

Accepted Answer

A)  x2 = -9y
B)  y2 = 36x
C)  x2 = -36y
D)  x2 = 36y
E)  y2 = -9xF) A) and D)
G) None of the above

Question 18

Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. ​
Vertices: (0,±7) ;focies: (0,±4) 
​

Accepted Answer

A)    x249+y233=1\frac { x ^ { 2 } } { 49 } + \frac { y ^ { 2 } } { 33 } = 149x2​+33y2​=1 
B)    x233+y249=1\frac { x ^ { 2 } } { 33 } + \frac { y ^ { 2 } } { 49 } = 133x2​+49y2​=1 
C)    x249+y233=−1\frac { x ^ { 2 } } { 49 } + \frac { y ^ { 2 } } { 33 } = - 149x2​+33y2​=−1 
D)    −x249+y233=1- \frac { x ^ { 2 } } { 49 } + \frac { y ^ { 2 } } { 33 } = 1−49x2​+33y2​=1 
E)    x233+y249=−1\frac { x ^ { 2 } } { 33 } + \frac { y ^ { 2 } } { 49 } = - 133x2​+49y2​=−1F) C) and D)
G) A) and D)

Question 19

Find the vertex and focus of the parabola for the given equation and select its graph.​  y=−3x2y = - 3 x ^ { 2 }y=−3x2  ​

Accepted Answer

A)  Vertex: (0,0)  Focus: (0,3)  
B)  Vertex: (0,0)  Focus: (0,-12)  
C)  Vertex: (0,0)  Focus: (0,-3)  
D)  Vertex: (0,0)  Focus:  (0,−112) \left( 0 , - \frac { 1 } { 12 } \right) (0,−121​)   
E)  Vertex: (0,0)  Focus:  (0,13) \left( 0 , \frac { 1 } { 3 } \right) (0,31​)    F) A) and E)
G) A) and B)

Question 20

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. directrix: x = 5

Accepted Answer

A)  x2 = -20y
B)  x2 = 20y
C)  x2 = 5y
D)  y2 = 5x
E)  y2 = -20xF) C) and E)
G) All of the above

Exam 60: Introduction to Conics Parabolas

Find the vertex and directrix of the parabola. $x ^ { 2 } - 14 x - 8 y + 73 = 0$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristics. Vertex: $( 0,2 )$ ;directrix: $y = 10$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristics. Vertex: $( - 5,5 )$ ;focus: $( - 5,0 )$

Correct Answer
verified

Find the vertex and focus of the parabola for the given equation and select its graph. $y = - 3 x ^ { 2 }$

Correct Answer
verified

Find the center and vertices which located on the major axis of the ellipse. $\frac { x ^ { 2 } } { 25 } + \frac { y ^ { 2 } } { 9 } = 1$

Correct Answer
verified

Identify the conic. $4 y ^ { 2 } - 8 x = 0$

Correct Answer
verified

Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin. Vertices: (±3,0) ;passes through the point $( 5 , \sqrt { 3 } )$

Correct Answer
verified

Give the standard form of the equation of the parabola with the given characteristics. vertex: (7,8) focus: (5,8)

Correct Answer
verified

Find the vertex and focus of the parabola from the given equation and select its graph. $2 x + y ^ { 2 } = 0$

Correct Answer
verified

Correct Answer
verified

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. focus: (0,-2)

Correct Answer
verified

Find the vertex and focus of the parabola. $x ^ { 2 } + 8 y = 0$

Correct Answer
verified

Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. Vertices: (0,±7) ;focies: (0,±4)

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. directrix: x = -9

Correct Answer
verified

Find the vertices and asymptotes of the hyperbola. $25 y ^ { 2 } - 4 x ^ { 2 } = 100$

Correct Answer
verified

Find the vertex,focus,and directrix of the parabola. $y ^ { 2 } = - 3 x$

Correct Answer
verified

Find the vertex and focus of the parabola from the given equation and select its graph. $y ^ { 2 } = 6 x$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Directrix: $y = 3$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. directrix: x = 5

Correct Answer
verified

Exam 60: Introduction to Conics Parabolas

Find the vertex and directrix of the parabola. x2−14x−8y+73=0x ^ { 2 } - 14 x - 8 y + 73 = 0x2−14x−8y+73=0

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the parabola with the given characteristics. ​ Vertex: (0,2) ( 0,2 ) (0,2) ;directrix: y=10y = 10y=10 ​

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the parabola with the given characteristics. ​ Vertex: (−5,5) ( - 5,5 ) (−5,5) ;focus: (−5,0) ( - 5,0 ) (−5,0) ​

Correct AnswerverifiedShow Answer

Find the vertex and focus of the parabola for the given equation and select its graph.​ y=−3x2y = - 3 x ^ { 2 }y=−3x2 ​

Correct AnswerverifiedShow Answer

Find the center and vertices which located on the major axis of the ellipse. x225+y29=1\frac { x ^ { 2 } } { 25 } + \frac { y ^ { 2 } } { 9 } = 125x2​+9y2​=1

Correct AnswerverifiedShow Answer

Identify the conic.​ 4y2−8x=04 y ^ { 2 } - 8 x = 04y2−8x=0 ​

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin. ​ Vertices: (±3,0) ;passes through the point ​ (5,3) ( 5 , \sqrt { 3 } ) (5,3​) ​

Correct AnswerverifiedShow Answer

Give the standard form of the equation of the parabola with the given characteristics. vertex: (7,8) focus: (5,8)

Correct AnswerverifiedShow Answer

Find the vertex and focus of the parabola from the given equation and select its graph.​ 2x+y2=02 x + y ^ { 2 } = 02x+y2=0 ​

Correct AnswerverifiedShow Answer

Correct AnswerverifiedShow Answer

Write an equation for a cross section of the parabolic ear (used to hear sounds from a distance) shown in the picture. ​ d = 2.25 inches

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. focus: (0,-2)

Correct AnswerverifiedShow Answer

Find the vertex and focus of the parabola. x2+8y=0x ^ { 2 } + 8 y = 0x2+8y=0 ​

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. ​ Vertices: (0,±7) ;focies: (0,±4) ​

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. directrix: x = -9

Correct AnswerverifiedShow Answer

Find the vertices and asymptotes of the hyperbola. 25y2−4x2=10025 y ^ { 2 } - 4 x ^ { 2 } = 10025y2−4x2=100

Correct AnswerverifiedShow Answer

Find the vertex,focus,and directrix of the parabola.​ y2=−3xy ^ { 2 } = - 3 xy2=−3x ​

Correct AnswerverifiedShow Answer

Find the vertex and focus of the parabola from the given equation and select its graph.​ y2=6xy ^ { 2 } = 6 xy2=6x ​

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. ​ Directrix: y=3y = 3y=3 ​

Correct AnswerverifiedShow Answer

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. directrix: x = 5

Correct AnswerverifiedShow Answer

Find the vertex and directrix of the parabola. $x ^ { 2 } - 14 x - 8 y + 73 = 0$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristics. Vertex: $( 0,2 )$ ;directrix: $y = 10$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristics. Vertex: $( - 5,5 )$ ;focus: $( - 5,0 )$

Correct Answer
verified

Find the vertex and focus of the parabola for the given equation and select its graph. $y = - 3 x ^ { 2 }$

Correct Answer
verified

Find the center and vertices which located on the major axis of the ellipse. $\frac { x ^ { 2 } } { 25 } + \frac { y ^ { 2 } } { 9 } = 1$

Correct Answer
verified

Identify the conic. $4 y ^ { 2 } - 8 x = 0$

Correct Answer
verified

Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin. Vertices: (±3,0) ;passes through the point $( 5 , \sqrt { 3 } )$

Correct Answer
verified

Correct Answer
verified

Find the vertex and focus of the parabola from the given equation and select its graph. $2 x + y ^ { 2 } = 0$

Correct Answer
verified

Correct Answer
verified

Correct Answer
verified

Correct Answer
verified

Find the vertex and focus of the parabola. $x ^ { 2 } + 8 y = 0$

Correct Answer
verified

Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. Vertices: (0,±7) ;focies: (0,±4)

Correct Answer
verified

Correct Answer
verified

Find the vertices and asymptotes of the hyperbola. $25 y ^ { 2 } - 4 x ^ { 2 } = 100$

Correct Answer
verified

Find the vertex,focus,and directrix of the parabola. $y ^ { 2 } = - 3 x$

Correct Answer
verified

Find the vertex and focus of the parabola from the given equation and select its graph. $y ^ { 2 } = 6 x$

Correct Answer
verified

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Directrix: $y = 3$

Correct Answer
verified

Correct Answer
verified