A) Clearly, all three means are the same, since all confidence intervals include zero or nearly do so.
B) We can be 95% confident that the intervention mean is different from both the control mean and the information mean, and the control mean and the intervention mean are not different.
C) We can be sure that the intervention group is different from the control and information groups, and the information group is not different from the control group.
D) We can be confident that the intervention mean is different from the control mean and information mean, while the control mean and information mean are not different, but we do not know the confidence level.
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A company runs a three-day workshop on strategies for working effectively in teams. On each day, a different strategy is presented. Forty-eight employees of the company attend the workshop. At the outset, all 48 are divided into 12 teams of four. The teams remain the same for the entire workshop. Strategies are presented in the morning. In the afternoon, the teams are presented with a series of small tasks. The number of these tasks completed successfully, using the strategy taught that morning, is recorded for each team. The mean number of tasks completed successfully by all teams each day and the standard deviation are computed. The results follow.  The researchers did an ANOVA F test of the data and obtained the following results.
The researchers did an ANOVA F test of the data and obtained the following results. 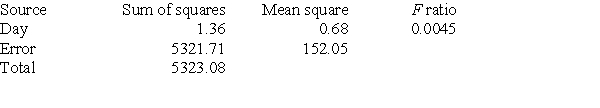 Which of the following conclusions is most reasonable?
Which of the following conclusions is most reasonable?
A) There is moderate evidence that the strategies taught are effective in increasing the number of tasks completed successfully for the first two days, but the effect appears to wear off.
B) An ANOVA F test is not appropriate for these data. Instead, the company should have done several tests to see if the number of tasks completed successfully differed for the three days. This analysis would have shown that the treatment was effective.
C) The data provide strong evidence that the mean number of tasks completed successfully differs for the three strategies taught.
D) The data appear to provide little or no evidence that the strategies taught differ in their effectiveness in helping teams complete tasks successfully.
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 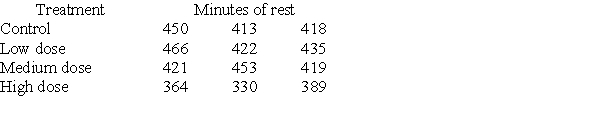 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 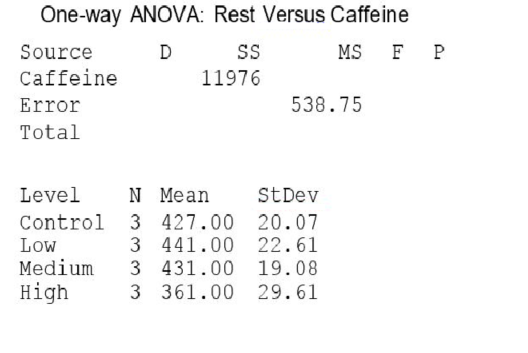 The value of the ANOVA F statistic for testing equality of the population means of the average rest time for the four caffeine levels is:
The value of the ANOVA F statistic for testing equality of the population means of the average rest time for the four caffeine levels is:
A) 2.78.
B) 4.73.
C) 4.82.
D) 7.41.
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Which of the following is a true statement about analysis of variance?
A) The null hypothesis test states that all population means i are the same.
B) The alternative is many-sided.
C) The F test assesses evidence for some differences among the population means i.
D) All of the answer options are correct.
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 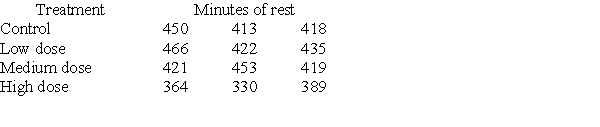 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 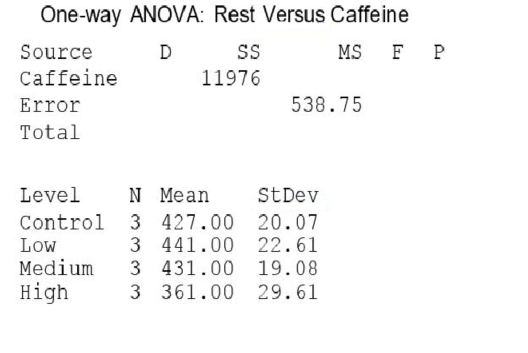 The pooled standard deviation is:
The pooled standard deviation is:
A) 22.84.
B) 23.21.
C) 91.37.
D) 2154.82.
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 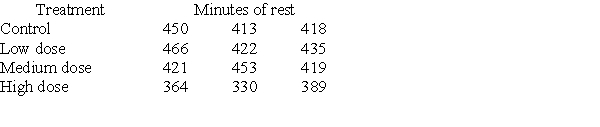 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The conclusion that you would draw from this test is:
The conclusion that you would draw from this test is:
A) accept the null hypothesis; all of the groups have the same mean.
B) fail to reject the null hypothesis; there is no evidence to suggest that the groups have different means.
C) reject the null hypothesis; all of the group means are different.
D) reject the null hypothesis; at least one of the groups has a mean that is different.
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 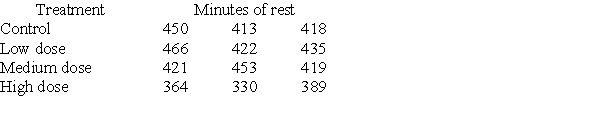 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The P-value of this test is:
The P-value of this test is:
A) greater than 0.1.
B) between 0.05 and 0.1.
C) less than 0.05.
D) It is not possible to determine the P-value from the information provided.
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The one-way ANOVA is a generalization of what other statistical test?
A) ANOVA is not related to any other tests.
B) the two-sample t test for independent means
C) the paired t test for independent means
D) Levene's test for differences between variations
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Showing 21 - 28 of 28
Related Exams